Man kan behöva mäta kurvradier på cykelbanor. Svängars snävhet påverkar framkomligheten och möjligheten att möta andra cyklister på ett säkert sätt. Här beskriver jag mina två mätmetoder som bara kräver tillgång till området närmast kanten.
Jag mäter alltid radien i kurvans innerkant. Det är där cyklistens utmaning är som störst, och det är också där man kan behöva cykla om man har möte, blir omkörd eller om den resterande delen är upptagen på något annat sätt. Den som vill mäta radien längre ut behöver förklara varför den svåraste delen inte ska räknas, men varför den ändå har byggts. Särskilt lådcyklar kan behöva styra med ett hjul nära innerkanten. Vet man innerkantens radie är det bara att plussa på den eventuella marginal man kan tänkas vilja ha när man redovisar kurvradier. Det kan ju läsaren få göra själv!
De två mätmetoderna jag vill beskriva har en gemensam grund men stör cykeltrafiken olika mycket. Jag kallar dem kordametoden och tangentmetoden.
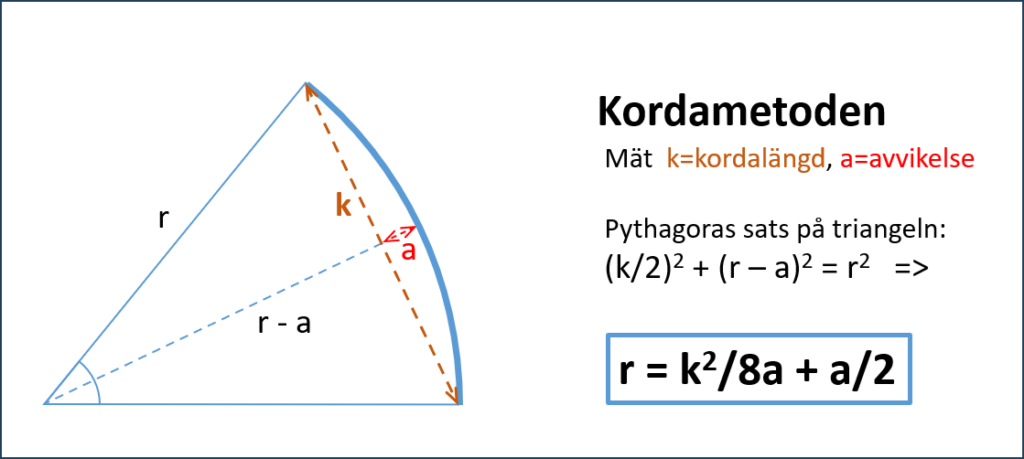
Kordametoden

Måttbandet ligger som en korda på cykelbanans innerkant. I mitten min tumstock för mätning av max avvikelse. Engelbrektsgatan vid Park Avenue i Göteborg.
Kordametoden är lämplig om det inte finns hinder att lägga ut en rak korda. Marken under måttbandet bör vara någorlunda jämn och fri. Grästuvor krånglar till det, för att inte tala om träd eller elskåp. Cykeltrafiken störs minimalt vid mätning med kordametoden på innerkurva.
Lägg ett måttband rakt som i fotot. Sikta från ändan för att kolla rakheten och justera vid behov. Det är särskilt viktigt att kordans mitt inte är förskjuten. Mät hela kordans längd k och kurvans maximala avvikelse a på halva längden. Stoppa in i formeln nedan.
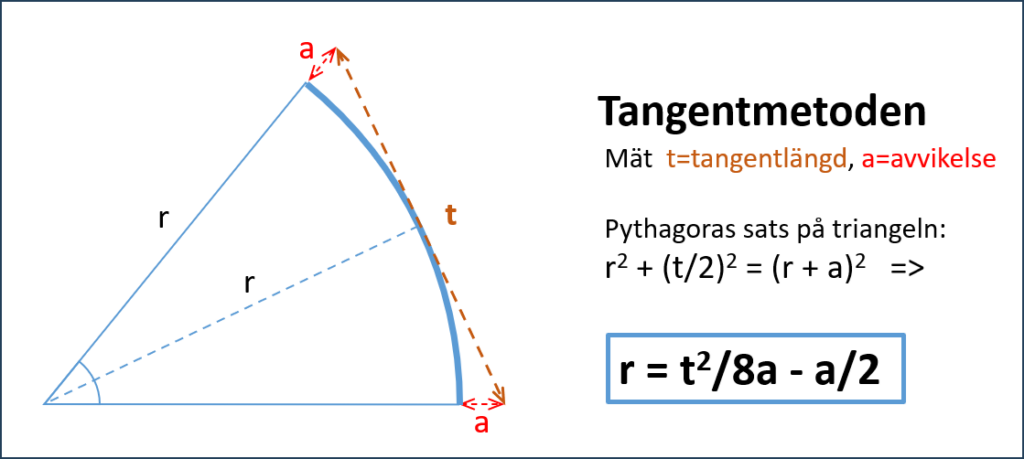
Tangentmetoden

I denna metod tangerar måttbandet cykelbanans innerkant. Närmast ses min tumstock för mätning av avvikelsen som ska vara lika stor i en slutpunkt på andra sidan. Engelbrektgatan vid Park Avenue i Göteborg.
Tangentmetoden är lämplig om platsen bjuder problem med att använda kordametoden. Cykeltrafiken störs lite mer vid mätning på innerkurva.
Lägg ett måttband som en tangent enligt fotot. Sikta från ändan för att kolla rakheten och justera vid behov. Det är särskilt viktigt att tangentens ändar inte är förskjutna. Välj ut en punkt nära tangentlinjens båda ändar som har samma avvikelse a till kurvans kant. Mät a vinkelrätt mot själva kurvkanten, inte vinkelrätt mot måttbandets tangentlinje. Mät tangentlängden t mellan de två avvikelsepunkterna. Stoppa in i formeln nedan.
Några tips
Jag har ännu bara mätt några få radier med dessa metoder, men ändå fått en del erfarenheter. Styva måttband brukar ha en hake vid 0 cm. Det är säkert risk för punktering om en cykel kör över haken. Jag har mjukt band med platt ända och rulle med vev. Rullen är röd och syns bra.
Jag använder träklossar för att hålla ändarna på plats. Klossarna är klädda med tjock mjuk gummi (plast?) med friktion för att fixera bandet och inte glida på banan när jag sträcker upp måttbandet. Har man bara rent trä räcker en minimal ojämnhet på markytan för att bandet ska löpa oberört i en glipa.
Med tangentmetoden skulle man teoretiskt kunna nöja sig med att bara mäta åt ena hållet från tangeringspunkten vilket ger måttet t/2. Men då riskerar man mycket sämre noggrannhet, speciellt om banans kurvlinje inte är perfekt cirkulär. Enskilda kantstenselement har inte säkert samma rundning som kurvan i stort. Så jag rekommenderar symmetrisk mätning.
Mäter man många radier kan man föra in sina mätningar i en Exceltabell med en mätning per rad och fixa en härledd kolumn för beräknad radie enligt formel ovan.
Hur noggrann bestämningen av radien blir är svårt att säga. Att det långa måttbandet ligger rakt är förstås viktigt, så sikta noga från ändan för att hitta och justera krokigheter. Och att bestämma en stor radie med ett avvikelsemått som bara är en bråkdel är förstås alltid en utmaning. Så försök göra mätområdet stort, men inte så stort så att man hamnar utanför den del av kurvan som ser ut att vara cirkulärt rundad. På ett foto som mina ovan kan man i efterhand kolla måttbandets rakhet och justera sitt avvikelsemått om bandet inte ligger helt rakt. Känner man bandets bredd blir det en bra måttstock för hur mycket man bör justera sitt avvikelsemått.
Om man konstaterar att cykelbanans bredd är densamma genom kurvan kan man förstås lika gärna mäta ytterkantens radie. Mät i så fall gärna båda!
Ett par fulkurvor
Här har antagligen gångbanans stenhällar fått bestämma geometrin. Hade man inte krävt enhetlig bredd på gatstensremsan kunde cykelbanans högra kantlinje ha löpt lika mjukt som den vänstra. I mina ögon ser den nu rätt tillknycklad ut.
Den som tror att man kan cykla så här kantigt bör testa själv. Effekten av en så vass utformning är i praktiken en kraftig avsmalning, motsvarande en getingmidja om banan hade varit rak. Ska man hålla sig innanför banans gränser i detta parti, måste man utnyttja hela bredden och svänga betydligt kraftigare än om linjeföringen hade varit mjuk.
Man ska säkert finna att bilar i parkeringsfickan bredvid inte heller kan svänga på detta kantiga sätt när de ska köra ut. En morgon med lite nysnö kan nog berätta en hel del om det. Med andra ord skapar denna utformning dödutrymmen för både cykel och bil.